
FORMULA INVERSA DELL'AREA DEL QUADRATO
La figura più semplice da studiare in geometria piana è senz'altro il quadrato perchè composto da 4 lati di egual lunghezza. Di conseguenza il perimetro è molto semplice da calcolare ed anche l'area, dato che essa dipende sempre dalla lunghezza di un lato. Il quadrato appartiene alla famiglia dei parallelogrammi ed è quello più semplice nella costruzione ed analisi. Presenta al suo interno 2 diagonali di ugual lunghezza che lo suddividono in 2 triangoli isosceli. La diagonale può essere quindi calcolata utilizzando il teorema di Pitagora e conoscendo i 2 cateti (lati del quadrato) che hanno uguale lunghezza. Oggi vediamo la formula diretta ed inversa dell'area del quadrato ma anche quella che riguarda il lato e la diagonale, oltre che quella riguardante il perimetro. Ad essa faremo seguire un semplice problema sullla figura del quadrato con soluzione che sarà molto facile eseguire. È un problema adatto a ragazzi di scuola media.
Il perimetro P del quadrato è uguale a :
P = l * 4 (dove l è un lato del quadrato)
Il lato, conoscendo il perimetro, sarà dato da :
l = P / 4
L'area A di un quadrato ha la seguente formula :
A = l^2 (lato l elevato alla seconda)
oppure :
A = (d^2) / 2 (dove d è la diagonale)
Di conseguenza le formule inverse dell'area A di un quadrato sono :
l = radice quadra di A
d = radice quadra di (A * 2)
Il valore della diagonale, proprio in seguito all'utilizzo del teorema di Pitagora, può essere ridotto alla formula :
d = l * radice quadra di 2
Quindi il valore del lato l conoscendo solo la diagonale d può essere trovato così :
l = d / radice quadra di 2
A questo indirizzo trovate le formule del quadrato scritte per bene e con i simboli tipici della potenza e della radice quadrata. Troverete anche un problema. Ma provate adesso ad eseguire questo scritto qui sotto a cui segue anche la soluzione.
PROBLEMA SUL CALCOLO DELL'AREA DI UN QUADRATO
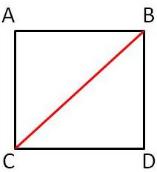
"Un quadrato ha la diagonale d pari al valore di 20 cm. Conoscendo questa, calcolate il valore dell'area A della figura geometrica. Inoltre trovate il valore dell'area A anche attraverso il valore del lato l"
Dati :
d = 20 cm
l = ?
A = ?
Soluzione :
A = (d^2) / 2 = (20^2) / 2 = 400 / 2 = 200 cm quadrati
l = d / radice quadra di 2 = 20 / 1,414 = 14,144 cm
A = l^2 = 14,144^2 = 200 cm quadrati
In geometria esistono moltissime altre figure sia piane che solide come il rombo, il trapezio, il cono, la sfera, la piramide e le ho descritte tutte con relative formule in diversi articoli che troverete cliccando sul link sotto. Ovviamente troverete anche problemi per esercitarvi ed utilizzare al meglio teoria e formule. Ma sempre seguendo il link sotto potrete giungere in una pagina da cui scegliere articoli non solo relativi alla geometria ma anche alla matematica, all'algebra e moltissimi articoli che riguardano la grammatica sia italiana che straniera con argomenti relativi a preposizioni, articoli determinativi ed indeterminativi, aggettivi, pronomi, avverbi, ecc... :







0 commenti:
Posta un commento