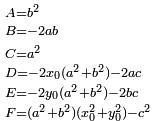FACILI PROBLEMI DI GEOMETRIA SULLE RETTE PARALLELE
Cercate problemi di geometria analitica sulle rette di tipo parallelo ? Lo studio delle rette sul piano cartesiano è abbastanza semplice se si conoscono alcuni concetti matematici oltre che geometrici. Una retta si dice parallela ad un'altra quando ogni suo punto risulta essere equidistante da ogni punto dell'altra retta posto di fronte proprio sulla sua perpendicolare. Ogni retta possiede una sua equazione e tramite questa possiamo sapere quanto è l'equidistanza tra due rette parallele poste nello stesso piano ma possiamo anche trovare la distanza di un punto di coordinate x,y che dista da esse. Oggi vediamo di eseguire un problema e far seguire ad esso 3 facili problemi di geometria da risolvere sulle rette parallele per ragazzi di scuola media, in particolare per ragazzi di terza media, oltre che per ragazzi di scuola superiore.
Come calcolare la distanza tra rette di tipo parallelo ? Ecco un esercizio svolto con risultato finale. La risoluzione di questo problema sul concetto di rette parallele nel piano cartesiano è la stessa da seguire nei 3 che trovate dopo anche se facendo diversi passaggi.
Su di un piano cartesiano vi sono due rette con equazioni :
6y - 3x + 6 = 0
y - 2x + 4 = 0
Lavoriamo sulla prima equazione che rappresenta la prima retta e troviamo il valore di y ponendo a 0 il valore di x. Otteniamo :
6y + 6 = 0
y = - 6/6 = - 1
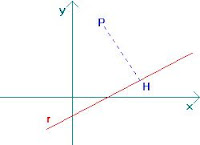
Il punto P posto sulla prima retta ha coordinate (0;-1). Ora dobbiamo verificare quale distanza vi sia tra questo punto e la seconda retta. Per far ciò utilizziamo una formula in cui x0 ed y0 saranno i valori del punto P trovato mentre a, b, c saranno i coefficienti della seconda equazione visto che l'equazione di una retta si scrive così : ax + by + c = 0.
La formula della distanza è :
sostituiamo i valori ed otteniamo :
d = [-2*(0) + 1*(-1) + 4] / radice quadra di [(-2)^2 + 1^2]
uguale a :
d = 3 / radice quadra di 5
Ovviamente affinchè le rette siano parallele anche altri punti trovati su di esse devono avere lo stesso valore relativo alla distanza. Per far ciò vi basta fare il contrario e cioè trovare il valore di y ponendo x a 0 nella seconda retta stavolta. Poi nella formula della distanza d utilizzeremo la seconda equazione. Se il risultato è identico a quello trovato la prima volta per la distanza allora le due rette sono parallele. Vi invito quindi a verificare che queste due rette, oggetto nell'esempio, siano parallele.
PRIMO PROBLEMA SULLE RETTE PARALLELE
"Verificare che le due rette di equazione 2y - 4x + 5 = 0 ; 3x - 4y - 8 = 0 siano parallele nel piano cartesiano"
SECONDO PROBLEMA SULLE RETTE PARALLELE
"Trovare l'equazione della retta parallela ad una di equazione 2x - 8y +1 = 0 e che passa dal punto P (-4;2) "
TERZO PROBLEMA SULLE RETTE PARALLELE
"Date due rette di equazione y=3x-4 ; y=3x+15, verificare che siano parallele disegnandole sul piano cartesiano"
Vi invito a seguire il link sotto se desiderate cercare altri articoli relativi alla geometria. Potrete scegliere tra argomenti legati a figure piane e solide, al
Teorema di Pitagora con esempi e problemi ed esercizi da svolgere. In più tanto materiale didattico sulla
matematica, algebra, aritmetica ed anche sulla grammatica sia italiana che straniera, in particolare inglese :
MATERIALE DIDATTICO DI ITALIANO GEOMETRIA MATEMATICA
Iscriviti al mio FEED RSS