
FORMULA DELL'AREA DEL PENTAGONO REGOLARE
Sappiamo che un pentagono è un poligono composto da 5 lati ed è regolare quando i 5 angoli interni ed i 5 lati sono uguali. Quale la misura di un singolo angolo interno ? Ogni angolo misura 108 gradi. Sotto troverete la formula. Se avete bisogno delle formule dirette ed inverse per il calcolo di perimetro ed area di un pentagono allora siete nel posto giusto perchè le troverete qui e troverete anche un semplice problema di geometria sul pentagono con la soluzione finale visto la semplicità di esso. Partiamo dalla formula dell'area del pentagono regolare che è la seguente :
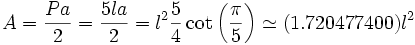
La formula sembra abbastanza complessa per alunni di scuola media ma in realtà dovete tener presente la prima parte di essa che permette di calcolare l'area A conoscendo soltanto il lato l o perimetro P del pentagono e il valore dell'apotema a. Quindi :
A = (P*a / 2) = (5*l*a) / 2
Il perimetro del pentagono regolare è dato da :
P = l+l+l+l+l = l*5
oppure dalla formula inversa dell'area A :
P = 2A / a
Più complesso calcolare il valore dell'apotema a del pentagono che può dipendere dal lato oppure dal raggio della circonferenza che circoscrive il pentagono in questione :


Ma se conosciamo area A e perimetro P o lato del pentagono regolare, allora l'apotema possiamo trovarla così :
a = 2A / P
Intanto il valore di ogni angolo interno alla figura piana in questione è dato da questa formula :

Adesso provate a risolvere questo semplicissimo problema in cui utilizzare le formule sopradette. Lasciate stare raggio, coseno e pigreco perchè utilizzerete solo valori del perimetro, lato e apotema utilizzando le formula più semplici.
SEMPLICE PROBLEMA SUL PENTAGONO REGOLARE

"Un pentagono possiede il lato l pari alla lunghezza del lato di un triangolo equilatero il cui perimetro P è pari a 60 cm. L'apotema a del pentagono è lunga quanto il lato di un quadrato che possiede l'area A pari a 484 cm quadrati. Calcolate il valore dell'area A del pentagono regolare in questione"
Dati :
lp = lt (lato pentagono uguale lato triangolo)
Pt = 60 cm (perimetro triangolo equilatero)
a = lq (apotema pentagono uguale lato quadrato)
Aq = 484 cm quadrati (area quadrato)
Ap = ?
Soluzione :
lp = lt (lato pentagono uguale lato triangolo)
lt = P / 3 = 60 / 3 = 20 cm
lp = 20 cm
a = lq (apotema pentagono uguale lato quadrato)
lq = radice quadra di A = radice quadra di 484 = 22 cm
a = 22 cm
Ap = (5 * l * a) / 2 = (5 * 20 * 22) / 2 = 2200 / 2 = 1100 cm quadrati
Se desiderate trovare altri problemi con formule, teoria ed esempi su diverse figure geometriche sia piane che solide allora non vi resta che eseguire una ricerca nel blog oppure cliccare sul link sotto che vi porterà in una pagina con tantissimi articoli da scegliere anche sulla matematica, algebra e sulla grammatica italiana e straniera con moltissimo materiale per poter svolgere al meglio analisi logico-grammaticali :







0 commenti:
Posta un commento