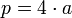LE FORMULE DIRETTE ED INVERSE DEL PRISMA
Oggi vediamo di parlare di una figura solida davvero molto particolare ed affascinante : il prisma. Esattamente oggi vedremo le formule del prisma a base quadrata, cioè avente per base un quadrato con quindi 4 lati uguali. Un prisma può avere una base anche triangolare, pentagonale, esagonale, ecc... Per calcolare il volume del prisma, la sua area laterale e totale bisogna quindi partire dalla base. Le formule del prisma avente base quadrata sono le seguenti.
Il perimetro P di base sarà dato da :
P = lx4
dove l è il lato del quadrato alla base. L'area di base sarà ovviamente l'area del quadrato data da :
Ab = lxl = l^2
quindi il lato che moltiplica se stesso oppure elevato alla seconda. Le facce laterali del prisma a base quadrata saranno 4 ed in base alla loro altezza formeranno dei rettangoli oppure quadrati (nel caso l'altezza corrisponda al lato del quadrato di base). L'area di una faccia laterale è :
Al = lxh
cioè la base di ogni faccia moltiplicata per l'altezza. L'area laterale di una faccia moltiplicata per 4 ci fornisce il valore totale dell'area laterale :
Al tot = Alx4
Per trovare l'area totale del prisma dobbiamo sommare l'area totale laterale a quella di base moltiplcata per due. Infatti il prisma possiede 2 basi opposte ed uguali. Le formule del prisma però non terminano qui perchè dobbiamo vedere come calcolare il volume di un prisma. Ecco la formula :
V = Abxh
L'area di base (quindi del quadrato) che moltiplica l'altezza
h del prisma. Un
prisma a base quadrata è detto
regolare e viene anche detto
parallelepipedo se ha base quadrata, triangolare oppure rettangolare. Credo che
le formule dirette ed inverse del prisma a base quadrata siano veramente semplici da trovare, partendo da quelle su scritte. Quindi non vi resta che esercitarvi utilizzandole per il problema che trovate sotto. Copiate la traccia sul quaderno, fate un bel prisma a base quadrata ed eseguite il tutto.
PROBLEMA SUL PRISMA A BASE QUADRATA
"Un prisma a base quadrata possiede il lato l di base pari a 4 cm. L'altezza h del prisma è il doppio del lato l di base. Calcolate l'area di base Ab, l'area laterale totale, l'area totale del prisma e il volume di quest'ultimo"
Se desiderate leggere articoli con teoria, formule e vari problemi relativi ad altre figure geometriche non vi resta che andare all'articolo indicato sotto da cui poter accedere a diversi altri articoli sulla geometria, sulla metematica, con espressioni, equazioni, ecc... ma anche sull'italiano e la grammatica, con analisi grammaticale e logica di frasi e testi, esercizi sui complementi e gli aggettivi, ecc... :
Iscriviti al mio FEED RSS