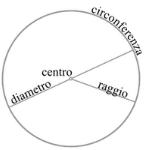
COME RISOLVERE PROBLEMI DI GEOMETRIA PIANA SULLA CIRCONFERENZA
Come fare a risolvere problemi di geometria analitica sulla figura piana della circonferenza ? La risoluzione dei problemi può avvenire anche grazie all'utilizzo di programmi del tipo DERIVE ma più esercizi fate voi personalmente e meglio è. Gli esercizi svolti di geometria sul cerchio o circonferenza sono la cosa migliore per imparare a risolverne anche di complessi. Se cercate semplici problemi di geometria per la scuola media ed in particolare per la classe terza media sulla figura piana della circonferenza già svolti, allora oggi vi offrirò le formule dirette da cui trarre quelle inverse e risolveremo anche un facile problema con esse. Seguirà poi un problema da risolvere con calma a casa.
Ecco le formule del cerchio che riguardano circonferenza, area e raggio. La circonferenza si calcola utilizzando il valore del raggio che moltiplica il valore 2 ed il valore di pigreco che sappiamo essere uguale a circa 3,14 ma che spesso rimane come costante nelle formule.

L'area A invece deriva dalla moltiplicazione del valore prima trovato della circonferenza (perimetro del cerchio) per il valore del raggio r o del valore del diametro/2 (il diametro è il doppio del raggio). Il tutto va diviso per il valore 2 e semplificando otteniamo il raggio r al quadrato che moltiplica pigreco.

Vediamo come calcolare il raggio r della circonferenza conoscendo il perimetro P :
r = P / 2 pigreco
Se invece abbiamo già il valore dell'area A, il raggio si trova con questa formula inversa :
r = radice quadrata (A / pigreco)
Adesso che conoscete le formule dirette ed inverse del cerchio proviamo a risolvere prima un semplice problema insieme e poi vi lascio con uno da copiare sul quaderno e da risolvere da soli.
RISOLUZIONE DI UN PROBLEMA SULLA CIRCONFERENZA
"Una circonferenza ha il perimetro P pari a 20 cm. Trovare la lunghezza del raggio r, del diametro d e dell'area A"
Soluzione :
r = P / 2π = 20 / 2π = 10π cm
d = r * 2 = 10π * 2 = 20π cm
A = πr² = π10² = 100π cm²
PROBLEMA SULLA CIRCONFERENZA DA RISOLVERE
"Un cerchio ha l'area A del valore di 80 metri quadri. Il suo diametro è pari alla lunghezza del lato l di un quadrato avente perimetro pari a 40 cm. Calcolate il valore della circonferenza e quindi del perimetro del cerchio"
Cercate altro sulla geometria ? Cercate formule, teoria e problemi su altre figure piane come il rettangolo, triangolo, parallelogramma, rombo oppure su figure solide come il cubo, la piramide, il cono, ecc... ? Allora seguite il link sotto e vi ritroverete in una pagina da dove poter scegliere tra decine di articoli relativi alla geometria ma non solo, anche alla matematica ed alla grammatica italiana e straniera con numerosissimi esercizi :







0 commenti:
Posta un commento