COME SI CALCOLA LA DISTANZA DI UN PUNTO DA UNA RETTA

COME SI CALCOLA LA DISTANZA DI UN PUNTO DA UNA RETTA

Cosa è la retta e cosa il punto ? Un punto non è altro che una entità adimensionale nello spazio e può essere visto come una coordinata. Infiniti punti formano una retta. La retta è infatti uno degli elementi alla base della geometria di Euclide. Una retta non ha dimensioni e non ha spessore ma è composta da infiniti punti che la rendono illimitata da entrambi i suoi lati. Ma come fare per calcolare la distanza di un punto qualsiasi da una retta ? Come si calcola la distanza di un punto non appartenente ad una retta ? Oggi vedremo come fare e quali formule utilizzare e poi potrete esercitarvi con un semplice problema sulla distanza tra punto e retta.

DEFINIZIONE DI DISTANZA DI UN PUNTO DA UNA RETTA

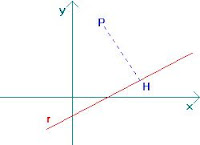
Data una retta r ed un punto P che non appartiene ad essa, la distanza del punto P da suddetta retta r è il segmento perpendicolare che parte dal punto e giunge sulla retta.

Nell' immagine sopra potete vedere che il segmento perpendicolare è indicato dalle lettere PH sul piano cartesiano. Supponiamo ora di avere su di un piano cartesiano un punto P di coordinate x0 , y0 ed una retta di equazione implicita ax + by + c = 0. La distanza d che non è altro che il segmento PH nel disegno sopra, si calcola così :

Per comprendere al meglio il tutto vediamo un semplice problema su questo argomento che vi aiuterà nel risolvere altri che vi verranno dati a scuola e che riguarderanno punto e retta in un piano cartesiano. Vi consiglio di copiare il tutto sul quaderno per meglio comprendere i passaggi da svolgere. Dopo il problema svolto troverete la traccia di un altro che voi stessi dovrete svolgere.

PROBLEMA SVOLTO SU PUNTO E RETTA

"Calcolate la distanza tra il punto P di coordinate (-3;5) e la retta r di equazione 4x - y + 8 = 0"

Dunque applichiamo la formula per il calcolo della distanza d sostituendo alle incognite i valori che possediamo. Otteniamo :

d = [4 * (-3) - (1 * 5) + 8] / rad. quadra di [4^2 + (- 1)^2]

-12 - 5 + 8 / rad. quadra di [8 + 2]

-9 / rad. quadra di [10]

PROBLEMA DA ESEGUIRE SU PUNTO E RETTA

"Calcolate la distanza tra il punto P di coordinate (-4;7) e la retta r di equazione 6x - y + 3 = 0"

Se desiderate trovare problemi vari sulla geometria piana e solida applicata a numerose figure come il rombo, il trapezio, il cono, il prisma, il cubo, ecc... allora seguite i link sotto ma soprattutto l'ultimo che vi porterà in una pagina da cui selezionare articoli vari anche di grammatica italiana e matematica e non solo di geometria :

PROBLEMI DI GEOMETRIA PER LE CLASSI MEDIE
DOVE RISOLVERE ONLINE PROBLEMI GEOMETRICI
PROBLEMI GEOMETRICI PER LA CLASSE TERZA MEDIA
ARTICOLI DI GEOMETRIA GRAMMATICA MATEMATICA

Iscriviti al mio FEED RSS