
"Ho bisogno di un problema sul quadrato che utilizza l'enunciato del teorema di Pitagora. Sapete dirmi, suggerirmi un semplice problema di geometria sulla figura del quadrato che fa uso delle formule del Teorema di Pitagora e che possiede la soluzione ? Dove posso trovare un problema risolto sul quadrato e sul Teorema di Pitagora ad esso applicato ?" Sapete cosa è e cosa dice il famoso Teorema di Pitagora ? A cosa serve questo teorema e quali formule applicare quando dobbiamo utilizzarlo per risolvere un problema di matematica o geometria ? Oggi vediamo di parlare di una figura geometrica basilare e cioè del quadrato, applicando ad esso proprio questo teorema. Spieghiamo prima l'enunciato del teorema e poi vediamo un facile problema per ragazzi di scuola media sul quadrato con il Teorema di Pitagora applicato.
TEOREMA DI PITAGORA - ENUNCIATO
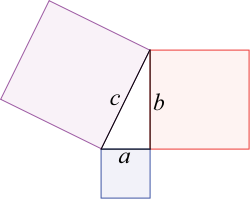
Questo teorema dice che c'è una relazione tra i 3 lati di un qualsiasi triangolo (o quasi), lati che vengono chiamati cateti ed ipotenusa. L'ipotenusa è il lato più lungo tra i 3 lati. L'enunciato del teorema di Pitagora dice che l'area A del quadrato costruito sull'ipotenusa è la somma delle 2 aree costruite sui cateti. Osservate il disegno qui sotto per comprendere la regola euclidea :
TEOREMA DI PITAGORA - CALCOLO IPOTENUSA E CATETI


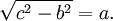
Semplicemente il valore dell'ipotenusa e cioè del lato maggiore tra i 3 è dato dalla somma dei 2 cateti al quadrato e posti sotto radice quadrata. Invece i 2 cateti si calcolano sottraendo al quadrato dell'ipotenusa il valore dell'altro cateto sempre al quadrato ed il tutto sempre sotto radice quadrata. Questo teorema è talmente importante da essere utilizzato per risolvere numerosissimi problemi di geometria piana. Qualsiasi figura geometrica all'interno della quale possiamo costruire un triangolo rettangolo e quindi un triangolo con un angolo di 90 gradi, può trovare l'applicazione del Teorema di Pitagora.
Ecco quindi come fare per risolvere un semplice problema sulla figura del quadrato usando proprio le formule del teorema succitato.
PROBLEMA SUL TEOREMA DI PITAGORA
Se non ricordate le formule del triangolo per il calcolo di perimetro ed area, allora leggete gli articoli qui sotto, dove troverete anche altri problemi su cui applicare la definizione e le formule del teorema pitagorico: Tramite l'ultimo link invece potrete accedere ad una pagina in cui scegliere tra diversi argomenti relativi alla grammatica italiana ed inglese, alla matematica e geometria :

Il quadrato costruito sull'ipotenusa c è grande quanto la somma delle 2 aree costruite sui 2 cateti a e b. Perchè il teorema di Pitagora possa trovare applicazione, tra i 2 cateti deve formarsi un angolo retto (90 gradi) interno al triangolo. I 2 cateti devono essere perpendicolari. Le formule del teorema di Pitagora sono queste.
TEOREMA DI PITAGORA - CALCOLO IPOTENUSA E CATETI


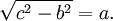
Semplicemente il valore dell'ipotenusa e cioè del lato maggiore tra i 3 è dato dalla somma dei 2 cateti al quadrato e posti sotto radice quadrata. Invece i 2 cateti si calcolano sottraendo al quadrato dell'ipotenusa il valore dell'altro cateto sempre al quadrato ed il tutto sempre sotto radice quadrata. Questo teorema è talmente importante da essere utilizzato per risolvere numerosissimi problemi di geometria piana. Qualsiasi figura geometrica all'interno della quale possiamo costruire un triangolo rettangolo e quindi un triangolo con un angolo di 90 gradi, può trovare l'applicazione del Teorema di Pitagora.
Ecco quindi come fare per risolvere un semplice problema sulla figura del quadrato usando proprio le formule del teorema succitato.
PROBLEMA SUL TEOREMA DI PITAGORA
"Un quadrato presenta il lato di 3 cm. Calcolate perimetro, area e diagonale di questo quadrato."
Dunque sappiamo che il perimetro del quadrato è dato dal lato l che viene moltiplicato per 4. Quindi in questo caso :
P = l * 4 = 3 * 4 = 12 cm
La formula per il calcolo della sua area invece è data dal valore del lato l al quadrato e quindi in questo caso :
A = l^2 = 3^2 = 9 cm quadrati
Bene, per calcolare la diagonale ci avvaliamo proprio di una delle formule del Teorema di Pitagora perchè tracciando una delle due diagonali il quadrato si divide in due triangoli rettangoli perfettamente identici. L'ipotenusa di ogni triangolo è proprio la diagonale ed i cateti sono i lati del quadrato che sono identici, tutti e 4 di uguale dimensione. Quindi la diagonale sarà uguale a :
d = (l^2 + l^2) tutto sotto radice quadrata = (3^2 + 3^2) tutto sotto radice quadrata = (9 + 9) tutto sotto radice quadrata = (18) tutto sotto radice quadrata = 4,2426 cm
Sotto radice troviamo la somma della potenza al quadrato dei 2 cateti che altro non sono che il lato del quadrato, quindi troviamo 18 la cui radice quadrata è appunto 4,2426 cm.
Dunque sappiamo che il perimetro del quadrato è dato dal lato l che viene moltiplicato per 4. Quindi in questo caso :
P = l * 4 = 3 * 4 = 12 cm
La formula per il calcolo della sua area invece è data dal valore del lato l al quadrato e quindi in questo caso :
A = l^2 = 3^2 = 9 cm quadrati
Bene, per calcolare la diagonale ci avvaliamo proprio di una delle formule del Teorema di Pitagora perchè tracciando una delle due diagonali il quadrato si divide in due triangoli rettangoli perfettamente identici. L'ipotenusa di ogni triangolo è proprio la diagonale ed i cateti sono i lati del quadrato che sono identici, tutti e 4 di uguale dimensione. Quindi la diagonale sarà uguale a :
d = (l^2 + l^2) tutto sotto radice quadrata = (3^2 + 3^2) tutto sotto radice quadrata = (9 + 9) tutto sotto radice quadrata = (18) tutto sotto radice quadrata = 4,2426 cm
Sotto radice troviamo la somma della potenza al quadrato dei 2 cateti che altro non sono che il lato del quadrato, quindi troviamo 18 la cui radice quadrata è appunto 4,2426 cm.
Se non ricordate le formule del triangolo per il calcolo di perimetro ed area, allora leggete gli articoli qui sotto, dove troverete anche altri problemi su cui applicare la definizione e le formule del teorema pitagorico: Tramite l'ultimo link invece potrete accedere ad una pagina in cui scegliere tra diversi argomenti relativi alla grammatica italiana ed inglese, alla matematica e geometria :








0 commenti:
Posta un commento