
"Ho la necessità di trovare e copiare un problema sulla figura del triangolo rettangolo che utilizza il teorema di Pitagora. Sapete dirmi, suggerirmi dove cercare un semplice problema di geometria sulla figura del triangolo rettangolo che fa uso delle formule del Teorema di Pitagora e possibilmente con la soluzione ? Dove posso trovare un problema risolto con la spiegazione di tutti i passaggi, le formule da usare sul triangolo rettangolo e sul Teorema di Pitagora ad esso applicato ?" Sapete cosa è e cosa dice il famoso Teorema di Pitagora ? A cosa serve questo teorema e quali formule si utilizzano quando dobbiamo utilizzarlo per risolvere un problema di matematica o geometria ? Applichiamo oggi questo importantissimo teorema alla figura geometrica piana del triangolo rettangolo. Dopo aver spiegato l'enunciato del teorema vedremo quindi di risolvere passo per passo un facile problema sul triangolo rettangolo per ragazzi di scuola media con il Teorema di Pitagora con soluzione finale.
TEOREMA DI PITAGORA - ENUNCIATO
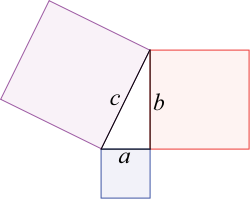
Il teorema dice che esiste una relazione tra i 3 lati di un triangolo purchè questo abbia almeno un angolo interno pari a 90 gradi. I lati che vengono chiamati cateti ed ipotenusa. L'ipotenusa è il lato più lungo tra i 3 lati. L'enunciato del teorema di Pitagora dice che l'area A del quadrato costruito sull'ipotenusa è la somma delle 2 aree costruite sui cateti. Ecco un semplice ma efficace disegno sotto per comprendere il tutto :
TEOREMA DI PITAGORA - CALCOLO IPOTENUSA E CATETI


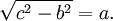
Quindi se vogliamo calcolare il valore dell'ipotenusa esso sarà dato dalla radice quadrata della somma dei due cateti al quadrato. Invece ogni singolo cateto si calcola con la radice quadrata della differenza tra l'ipotenusa al quadrato e l'altro cateto al quadrato. Questo teorema è fondamentale per poter risolvere molti problemi di geometria piana. Per qualsiasi figura geometrica all'interno della quale possiamo costruire un triangolo rettangolo e quindi un triangolo con un angolo di 90 gradi, possiamo applicare il Teorema di Pitagora.
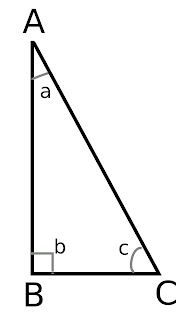
Ora passiamo ad affrontare la risoluzione di un semplicissimo problema che utilizza queste formule applicate ad un triangolo rettangolo. Sotto trovate la figura e con b viene indicato l'angolo retto di 90 gradi quindi. Possiamo perciò applicare il succitato teorema.
PROBLEMA SUL TEOREMA DI PITAGORA
Se cercate altri argomenti relativi alla geometria e quindi ancora sull'uso del teorema di Pitagora applicato ad altre figure piane, allora seguite i link sotto. Se invece seguite l'ultimo dei 3 link qui sotto potrete ricercare altro materiale didattico sulla matematica, sulla grammatica italiana ed inglese con tantissima teoria corredata da esempi, esercizi svolti e da svolgere e frasi pronte su moltissime regole grammaticali tra cui proposizioni, coniugazione di verbi, avverbi, aggettivi, preposizioni, ecc... :

Il quadrato costruito sull'ipotenusa c (e quindi avente come lato proprio la lunghezza dell'ipotenusa) è grande quanto la somma delle 2 aree costruite sui 2 cateti a e b. Perchè il teorema di Pitagora possa trovare applicazione, tra i 2 cateti deve formarsi un angolo retto (90 gradi) interno al triangolo. I 2 cateti devono essere perpendicolari. Ecco qui sotto le formule per calcolare i due cateti ed anche l'ipotenusa.
TEOREMA DI PITAGORA - CALCOLO IPOTENUSA E CATETI


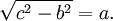
Quindi se vogliamo calcolare il valore dell'ipotenusa esso sarà dato dalla radice quadrata della somma dei due cateti al quadrato. Invece ogni singolo cateto si calcola con la radice quadrata della differenza tra l'ipotenusa al quadrato e l'altro cateto al quadrato. Questo teorema è fondamentale per poter risolvere molti problemi di geometria piana. Per qualsiasi figura geometrica all'interno della quale possiamo costruire un triangolo rettangolo e quindi un triangolo con un angolo di 90 gradi, possiamo applicare il Teorema di Pitagora.
Ora passiamo ad affrontare la risoluzione di un semplicissimo problema che utilizza queste formule applicate ad un triangolo rettangolo. Sotto trovate la figura e con b viene indicato l'angolo retto di 90 gradi quindi. Possiamo perciò applicare il succitato teorema.
PROBLEMA SUL TEOREMA DI PITAGORA
"Un triangolo rettangolo presenta il lato maggiore (ipotentusa) di 25 cm mentre il suo cateto minore AB ha una lunghezza di 20 cm. Calcolate il valore del cateto rimanente, perimetro ed area di questo triangolo."
Dalle formule sopra indicate possiamo subito calcolare il cateto BC dato che abbiamo il valore dell'ipotenusa AC e quello dell'altro cateto AB :
BC = (AC^2 - AB^2) tutto sotto radice quadrata = (25^2 - 20^2) tutto sotto radice quadrata = (625 - 400) tutto sotto radice quadrata = (225) tutto sotto radice quadrata = 15 cm
La formula per il calcolo della sua area invece è data dalla base BC che moltiplica l'altezza rappresentata da AB ed il tutto diviso per 2 e quindi in questo caso :
A = (BC * AB) / 2 = (15 * 20) / 2 = 150 cm quadrati
Una volta che conosciamo il valore dei 3 lati e quindi di ipotenusa e cateti, il calcolo del perimetro è semplicissimo perchè basta sommare tra loro i valori. Quindi il perimetro sarà uguale a :
P = AB + BC + AC = 20 + 15 + 25 = 60 cm
Sotto radice troviamo la somma della potenza al quadrato dei 2 cateti che altro non sono che il lato del quadrato, quindi troviamo 18 la cui radice quadrata è appunto 4,2426 cm.
Dalle formule sopra indicate possiamo subito calcolare il cateto BC dato che abbiamo il valore dell'ipotenusa AC e quello dell'altro cateto AB :
BC = (AC^2 - AB^2) tutto sotto radice quadrata = (25^2 - 20^2) tutto sotto radice quadrata = (625 - 400) tutto sotto radice quadrata = (225) tutto sotto radice quadrata = 15 cm
La formula per il calcolo della sua area invece è data dalla base BC che moltiplica l'altezza rappresentata da AB ed il tutto diviso per 2 e quindi in questo caso :
A = (BC * AB) / 2 = (15 * 20) / 2 = 150 cm quadrati
Una volta che conosciamo il valore dei 3 lati e quindi di ipotenusa e cateti, il calcolo del perimetro è semplicissimo perchè basta sommare tra loro i valori. Quindi il perimetro sarà uguale a :
P = AB + BC + AC = 20 + 15 + 25 = 60 cm
Sotto radice troviamo la somma della potenza al quadrato dei 2 cateti che altro non sono che il lato del quadrato, quindi troviamo 18 la cui radice quadrata è appunto 4,2426 cm.
Se cercate altri argomenti relativi alla geometria e quindi ancora sull'uso del teorema di Pitagora applicato ad altre figure piane, allora seguite i link sotto. Se invece seguite l'ultimo dei 3 link qui sotto potrete ricercare altro materiale didattico sulla matematica, sulla grammatica italiana ed inglese con tantissima teoria corredata da esempi, esercizi svolti e da svolgere e frasi pronte su moltissime regole grammaticali tra cui proposizioni, coniugazione di verbi, avverbi, aggettivi, preposizioni, ecc... :







0 commenti:
Posta un commento