PROBLEMI TEOREMA DI PITAGORA TRIANGOLO RETTANGOLO

PROBLEMI TEOREMA DI PITAGORA TRIANGOLO RETTANGOLO

Se siete giunti qui forse starete cercando o la teoria sul famoso teorema di Pitagora sui triangoli oppure problemi relativi a questo teorema applicabile sul triangolo isoscele, scaleno, equilatero o anche sul rombo, problemi per applicare la regola ad esso legata. Avete trovato entrambe le cose perchè oggi vedremo di spiegare come funziona questo enunciato di geometria. In più vi darò alcuni semplici problemi su cui applicare il teorema di Pitagora, uno relativo al triangolo rettangolo ed uno al trapezio rettangolo.

Sono problemi di geometria su figure che di solito si studiano alle scuole medie ed in particolare in terza media, dove si studia appunto il teorema sopracitato. Ma cosa dice questo famoso teorema di Pitagora ? Ecco il suo enunciato :

"La somma delle 2 aree quadrate costruite sui 2 cateti è pari al valore dell'area del quadrato costruita sull'ipotenusa"

Dal disegno sopra capite che l'area del quadrato c è la somma delle 2 aree a e b. E si perchè quando parliamo di Pitagora parliamo di cateti ed ipotenusa. L'ipotenusa è il lato più lungo tra i 3 in un triangolo e si calcola in questo modo :

La lettera "c" corrisponde alla lettera "i" nella figura sopra, cioè all'ipotenusa. Quindi per calcolare l'ipotenusa dobbiamo conoscere la lunghezza dei 2 cateti che, al quadrato, sommati e posti sotto radice, ci danno il suo valore. Per il calcolo dei 2 cateti a e b conoscendo l'ipotenusa, le formule sono le seguenti :

Come capite quindi il cateto a corrisponde all'altezza del triangolo rettangolo. Ma adesso dobbiamo mettere in pratica le formule con problemi sul teorema di Pitagora e lo facciamo con uno sulla figura del triangolo rettangolo ed uno sulla figura del trapezio rettangolo. Da questi sarà semplice capire come applicare il teorema anche su un triangolo equilatero, isoscele, scaleno, che si formano anche in figure come il rettangolo oppure il trapezio o ancora rombo.

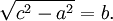
PROBLEMA TEOREMA DI PITAGORA TRIANGOLO RETTANGOLO

"Un triangolo rettangolo presenta la base b pari al valore del lato l di un quadrato avente area A pari a 25 cm quadrati. Il suo lato obliquo (ipotenusa) è lungo 9 cm. Calcolate il valore dell'altezza h, corrispondente all'altro cateto ed inoltre area A e perimetro P del triangolo stesso"

Soluzione :

h=7,48 cm (circa)

P=21,48 cm

A=18,7 cm quadrati

PROBLEMA TEOREMA DI PITAGORA TRAPEZIO RETTANGOLO

"Un trapezio rettangolo presenta la base minore b pari a 6 cm e quella maggiore B il doppio della minore. Il lato obliquo (ipotenusa) è lungo 9 cm. Calcolate quindi l'altezza h del trapezio rettangolo oltre alla sua area A e al suo perimetro P"

Soluzione :

h=6,70 cm (circa)

P=33,7 cm

A=60,3 cm quadrati

Studiatevi per bene il teorema di Pitagora con le sue formule prima di provare a risolvere i problemi. State attenti all'uso della radice quadrata e all'elevamento alla potenza del 2. Ricopiate i 2 problemi sul quaderno, disegnate per bene le figure geometriche, scrivete i dati e buono studio !!! Se desiderate cimentarvi in altri problemi di geometria su diverse figure geometriche, allora andate a questa pagina del blog :

VARI PROBLEMI DI GEOMETRIA PER SCUOLE MEDIE

Iscriviti al mio FEED RSS