
FORMULE INVERSE DEL TRIANGOLO EQUILATERO
Oggi vediamo quali sono le formule inverse relative ad un triangolo che è quello equilatero. Innanzitutto facciamo un pò di teoria a cui seguiranno le formule e dopo un bel problemino da risolvere su questa figura geometrica che è tra le prime, dopo il quadrato ed il rettangolo, ad essere studiate alla scuole primarie e medie.
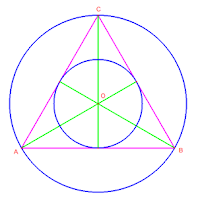
Un triangolo equilatero presenta tutti e 3 i lati di egual lunghezza e quindi anche gli angoli interni pari ciascuno a 60 gradi, visto che la somma totale deve dare 180 gradi. Un triangolo equilatero è perfettamente inscrivibile in un cerchio e circoscrivibile ad esso.
A questo punto vediamo le formule generali, che dipendono dal lato l , a cui seguiranno le formule inverse del triangolo equilatero :


Come vedete il perimetro P, l'altezza h e l'area A del triangolo dipendono tutte dal valore del lato l. Se abbiamo quello, allora possiamo calcolare tutto. Il problema insorge quando dobbiamo calcolare il lato l conoscendo perimetro, area e altezza. Le formule inverse del triangolo equilatero, per conoscere il lato sono quindi :
l = 2h / radice 3
l = P / 3
l = A/0,433 (tutto sotto radice quadrata)
La radice quadrata di 3 corrisponde al valore 1,7320 circa e il valore 0,433 viene fuori dalla formula sull'area A e corrisponde alla radice quadrata di 3 diviso il valore 4. Queste le formule inverse del triangolo equilatero. Abbasanza particolari e che comunque derivano dall'applicazione del teorema di Pitagora che vi invito ad approfondire qui :
Adesso vediamo di risolvere un problema, o meglio, sarete voi a risolverlo, ricopiandolo sul quaderno.
PROBLEMA SUL TRIANGOLO EQUILATERO
"Un triangolo equilatero presenta altezza h pari a 7 cm. Dopo aver calcolato il lato l del triangolo, trovate il valore dell'area A e del perimetro P"
Risultati :
l = 8,08 cm circa
P = 24,24 cm
A = 27,6 cm quadrati circa
Se volete potete anche provare a cimentarvi in altri problemi relativi al triangolo isoscele e rettangolo, studiandone prima la teoria :







0 commenti:
Posta un commento