
LE FORMULE DEL ROMBO
Il rombo è un pesce del Mar Mediterraneo ma anche una figura geometrica. Oggi vediamo proprio di parlare del rombo come figura in geometria. Il rombo altro non è che un quadrato schiacciato ai lati e come il quadrato presenta i 4 lati uguali tra loro. Le formule del rombo per calcolare perimetro ed area sono davvero semplici e fanno uso di 2 lunghezze che sono la diagonale maggiore e quella minore. Ciascuna unisce 2 dei 4 vertici all'interno del rombo stesso. Dopo aver visto le formule vi offrirò anche un problema da risolvere sul rombo. Ma adesso vediamo come calcolare il perimetro di un rombo :
FORMULE DEL ROMBO : PERIMETRO
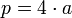
dove P sta per perimetro e a sta per lunghezza di un lato. Facile capire dunque che il lato moltiplicato per 4 ci da il valore del perimetro. Ma adesso vediamo come si fa a calcolare l'area di un rombo. Vi dico subito che diverse sono le formule, alcune più complesse, altre adatte a ragazzi di scuola media.
FORMULE DEL ROMBO : AREA N. 1
A = a x h
dove a è un lato del rombo ed h l'altezza di esso stesso.
FORMULE DEL ROMBO : AREA N. 2
A = (d1 x d2)/2
Le 2 diagonali, moltiplicate fra loro e divise per 2 ci danno il valore dell'area A del rombo.FORMULE DEL ROMBO : AREA N. 3
A = P x r
All'interno di un rombo è possibile inscrivere una circonferenza ed è per questo che l'area può essere calcolata moltiplicando il valore del perimetro P del rombo per il raggio r di questa circonferenza.FORMULE DEL ROMBO : AREA N. 4


PROBLEMA SUL ROMBO
"Un rombo possiede una diagonale d1 minore pari a 4 cm. La diagonale D2 (maggiore) è il doppio della diagonale minore. Sapendo che il lato a del rombo è lungo quanto la diagonale minore meno 1 cm, calcolate perimetro P e area A del rombo in questione"
Soluzione :
P = 12 cm
A = 16 cm quadrati
Se desiderate studiare altre figure geometriche ed affrontare diversi problemi di geometria relativi, allora provate a leggere questi altri articoli :







0 commenti:
Posta un commento