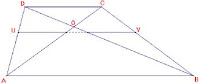
AREA E PERIMETRO DEL TRAPEZIO
Oggi parliamo del trapezio e vedremo come fare a calcolare area e perimetro del trapezio isoscele, area e perimetro del trapezio rettangolo e di quello scaleno. La differenza nelle formule si trova a livello del perimetro mentre per quanto riguarda l'area essa si calcola con la stessa formula per tutte e tre le figure.
FORMULE AREA E PERIMETRO TRAPEZIO RETTANGOLO

Il trapezio rettangolo possiede un angolo interno di 90 gradi e quindi 2 lati esattamente perpendicolari, uno di essi è l'altezza del trapezio. Le formule sono le seguenti :
A = [(b+B) x h]/2
P = B+b+h+l
La formula per il calcolo dell'area del trapezio viene dalla somma delle 2 basi che moltiplica il valore dell'altezza ed il tutto diviso 2. Il perimetro del trapezio rettangolo invece si calcola con la somma di base minore, base maggiore, altezza (che corrisponde ad un lato) ed il lato obliquo. Il lato obliquo può essere calcolato, conoscendo altezza e base minore e maggiore, con il teorema di Pitagora.
FORMULE AREA E PERIMETRO TRAPEZIO ISOSCELE
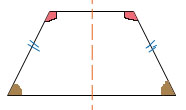
Il trapezio isoscele invece ha la caratteristica di avere 2 lati obliqui uguali e questo porta a calcolare area e perimetro del trapezio isoscele utilizzando queste 2 formule :
A = [(b+B) x h]/2
P = B+b+2l
Come vedete l'unica differenza con le formule del trapezio rettangolo sono nella formula del perimetro che presenta 2 volte il lato l visto che i 2 lati obliqui sono uguali.
FORMULE AREA E PERIMETRO TRAPEZIO SCALENO

Per quanto riguarda le formule di area e perimetro del trapezio scaleno, quella dell'area rimane identica come sopra mentre per il perimetro, essendo i 4 lati di diversa lunghezza, la formula diventa :
P = B+b+l1+l2
dove l1 corrisponde al lato AD in figura sopra ed l2 al lato CB. Anche qui possiamo applicare il teorema di Pitagora per calcolare questi lati conoscendo altezza e base maggiore e minore del trapezio.
Le differenze tra i vari trapezi sono queste. Ora non posso che indicarvi alcuni articoli dove descrivo al meglio le varie figure, articoli dove troverete teoria, formule e problemi per esercitarvi. In più, dato che il trapezio possiede delle diagonali ed avendone parlato in articoli precedenti, vi offro anche il link all'articolo dove capire come si calcola la diagonale di un trapezio :







0 commenti:
Posta un commento