DIAGONALE DEL ROMBO FORMULA
Come fare a calcolare una diagonale di un rombo ? Il rombo possiede 2 diagonali ed oggi vediamo come si calcola la diagonale più piccola e quella più grande del rombo. Vedremo insomma le formule dirette ed inverse del rombo. Sappiamo che un rombo è un tipo particolare di parallelogramma che possiede 4 lati uguali.
Vediamo come calcolare prima perimetro P ed area A di un rombo. Vi ricordo che l'area di un rombo può essere calcolata in svariati modi, con l'utilizzo, ad esempio dei seni degli angoli ma sotto vi indico tutte le formule. Eccole :
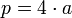
P rappresenta il perimetro che si calcola moltiplicando per 4 il valore di un lato a, essendo i lati di egual lunghezza. Adesso vediamo le diverse formule per calcolare l'area del rombo :
AREA N. 1
A = a x h
dove a è un sempre un lato del rombo ed h la sua altezza.
AREA N. 2
A = (d1 x d2)/2
La moltiplicazione delle 2 diagonali tra loro ed il tutto diviso il valore 2. Questo è uno dei modi più utilizzati per trovare l'area A.AREA N. 3
A = P x r
Siccome all'interno della figura geometrica del rombo è possibile inscrivere una circonferenza allora l'area può essere calcolata con la moltiplicazione tra perimetro rombo e raggio circonferenza.AREA N. 4
Questa è la formula più complessa che lasciamo stare visto che i miei articoli sono per ragazzi di scuola elementare e media. Quello che ci manca adesso è vedere come si calcola la diagonale del rombo. Le formule inverse per calcolare la diagonale vengono dalla seconda formula per il calcolo dell'area A :
A = (d1 x d2)/2
Le formule inverse sono :d1 = 2A/d2
d2 = 2A/d1
d2 = 2A/d1
Dobbiamo calcolare una diagonale conoscendone almeno una. Come fare quindi ? Utilizzando il teorema di Pitagora. Infatti le diagonali dividono il rombo in 4 triangoli rettangoli come da figura :
La diagonale più grande (in figura sopra AC) sarà il risultato della formula :
d2 = radice quadrata di [a^2 - (d1/2)^2]
Quindi la diagonale maggiore del rombo sarà uguale alla radice quadrata del lato a alla seconda (ipotenusa) meno il valore al quadrato della metà della diagonale minore (cateto). Per trovare la diagonale minore sapendo lato a e diagonale maggiore la formula è :
d1 = radice quadrata di [a^2 - (d2/2)^2]
Non sono formule complesse ma che richiedono attenzione nell'applicazione della formula del teorema di Pitagora. Adesso non vi resta che provare a risolvere questo semplice problema sul rombo.
PROBLEMA SUL ROMBO
"Un rombo ha la diagonale d1 minore pari a 4 cm. La diagonale d2 (maggiore) è il doppio della minore. Sapendo che il lato a del rombo è lungo come la diagonale minore meno 1 cm, calcolate perimetro P ed area A dela figura"
Soluzione :
P = 12 cm
A = 16 cm quadrati
Volete cimentarvi in altri problemi di geometria relativi ad altre figure semplici e complesse ? Allora seguite questi links e troverete teorie, formule e diversi problemi . L'ultimo link vi porta ad una sorta di indice del blog da dove poter scegliere articoli con esercizi di matematica, geometria, italiano, grammatica, ecc... :
CALCOLO AREA TRAPEZIO ISOSCELE
VOLUME DEL PARALLELEPIPEDO RETTANGOLO
ESERCIZI DI ITALIANO GRAMMATICA MATEMATICA GEOMETRIA
VOLUME DEL PARALLELEPIPEDO RETTANGOLO
ESERCIZI DI ITALIANO GRAMMATICA MATEMATICA GEOMETRIA
Iscriviti al mio FEED RSS 
0 commenti:
Posta un commento