
CALCOLARE LATO TRIANGOLO ISOSCELE
Come fare a calcolare il lato del triangolo isoscele, di un triangolo isoscele di cui conosciamo solamente il valore dell'altezza e della base ? Naturalmente utilizzando il famoso ed indispensabile teorema di Pitagora. Il teorema, per la verità già utilizzato in tempi antichi (Egizi) lavora su un triangolo che abbia un angolo retto, quindi di 90 gradi, al suo interno. Due dei 3 lati devono essere perpendicolari per poter parlare di ipotenusa e cateti. Vediamo un disegno di un triangolo rettangolo qui sotto :
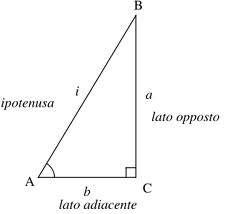
L'ipotenusa corrisponde al lato obliquo, cioè al lato più lungo mentre a e b corrispondono ai cateti, cioè ad altezza e base del triangolo rettangolo. Ma adesso torniamo al triangolo isoscele e a come fare per calcolare il suo lato, attraverso il teorema. Innanzitutto la definizione precisa del teorema è questa :
"L'area che si forma sul lato detto ipotenusa è la somma delle 2 aree che si formano sui lati detti cateti". Ecco l'immagine sotto :
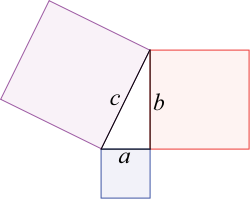
Ma il lato di un triangolo isoscele, cioè con 2 lati obliqui uguali, come si calcola, visto che il triangolo non è rettangolo ? Semplice, l'altezza che parte dal vertice del triangolo isoscele divide la figura in 2 triangoli rettangoli come in figura sotto :

A questo punto se consideriamo l'altezza come un cateto e metà della base come l'altro cateto, possiamo applicare il teorema di Pitagora, utilizzando la prima delle formule seguenti, dove c corrisponde al valore dell'ipotenusa cioè del lato obliquo :


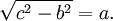
Ecco come calcolare il lato del triangolo isoscele. La somma dei 2 cateti al quadrato posta sotto radice ci da il valore dell'ipotenusa. Se conosciamo l'ipotenusa (lato obliquo) ed un cateto possiamo trovare il valore dell'altro, attraverso le formule inverse, quindi la seconda o terza su. Ma adesso voglio fornirvi un problema dove poter applicare il teorema pitagorico proprio per calcolare l'ipotenusa, quindi il lato obliquo di un triangolo isoscele.
PROBLEMA SUL TRIANGOLO ISOSCELE
"Un triangolo isoscele presenta l'altezza h pari al valore del lato l di un quadrato, la cui area A risulta essere di 81 cm quadrati. La base b del triangolo isoscele corrisponde a 7 cm. Calcolate il lato obliquo (ipotenusa) del triangolo, oltre al suo perimetro P ed area A"
Risultati :
lato obliquo = 9,65 cm circa
P = 26,3 cm circa
A = 31,5 cm quadrati
Spero ricordiate le formule per il calcolo di Area e Perimetro di un triangolo. Comunque vi offro il link per andare a trovarle insieme ad altri articoli dove trovare altri esercizi sul teorema di Pitagora :







0 commenti:
Posta un commento