ENUNCIATO DEL TEOREMA DI PITAGORA

ENUNCIATO DEL TEOREMA DI PITAGORA

Prima di scrivere la definizione del teorema di Pitagora diciamo subito che esso viene studiato principalmente e per la prima volta nelle scuole medie, quando si affronta la figura geometrica del triangolo, sia esso equilatero che isoscele, rettangolo o scaleno. Il teorema di Pitagora fa parte della geometria euclidea ed in realtà non fu scoperto dal matematico Pitagora ne tanto meno dimostrato. Questo teorema dimostra una relazione tra i 3 lati di un triangolo, permettendo la soluzione di diversi problemi dove viene richiesto di ricercare la lunghezza di uno di questi lati che vengono chiamati cateti ed ipotenusa.

L'ipotenusa è il lato più lungo tra i 3. L'enunciato del teorema di Pitagora dice che l'area A del quadrato costruito sull'ipotenusa è la somma delle 2 aree costruite sui cateti. Per meglio capire il concetto e la definizione del teorema di Pitagora, osservate questo disegno :

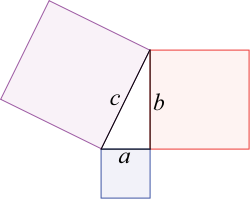
Il quadrato costruito sull'ipotenusa c è grande quanto la somma delle 2 aree costruite sui 2 cateti a e b. Perchè il teorema di Pitagora sia applicabile, tra i 2 cateti deve formarsi un angolo retto interno al triangolo. I 2 cateti devono essere quindi perfettamente perpendicolari. Ma, l'enunciato o definizione del teorema di Pitagora ci porta a delle formule che sono queste.

FORMULE DEL TEOREMA DI PITAGORA

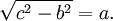
Dunque vediamo come l'ipotenusa c venga calcolata come la radice quadrata della somma del valore dei 2 cateti al quadrato. Ciascuno dei 2 cateti a e b invece vede la radice quadrata della differenza di ipotenusa e cateto al quadrato. Capire il teorema di Pitagora con le sue formule che non sono difficili, è importante per imparare ad eseguire molti problemi di geometria. Infatti questo teorema viene applicato anche a trapezi, rombi, insomma in quelle figure geometriche dove sia possibile costruire un triangolo rettangolo interno.

Ma adesso, dopo aver visto la definizione e le formule del teorema di Pitagora, un bel problema ad esso relativo non guasta. Provate ad risolverlo, dato anche che è molto semplice.

PROBLEMA SUL TEOREMA DI PITAGORA

"Un triangolo rettangolo presenta il cateto più piccolo pari alla lunghezza del lato l di un quadrato, la cui area A è 100 cm quadrati. Il cateto più grande del triangolo è il doppio del cateto più piccolo. Dopo aver trovato l'ipotenusa del triangolo, utilizzando il teorema di Pitagora, calcolate perimetro P ed area A del triangolo stesso"

Risultati :

ipotenusa = 22,36 cm circa

P = 52,36 cm circa

A = 100 cm quadrati

Se non ricordate le formule del triangolo per il calcolo di perimetro ed area, allora leggete questi miei articoli, dove troverete anche altri problemi su cui applicare la definizione e le formule del teorema pitagorico :

FORMULE DEL TRIANGOLO RETTANGOLO

PROBLEMI CON IL TEOREMA DI PITAGORA

Iscriviti al mio FEED RSS